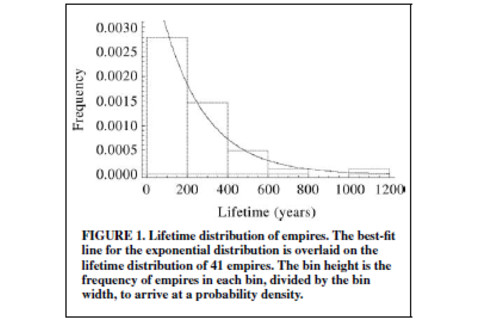
I was alerted to Samuel's Arbesman's new paper, The Life-Spans of Empires, by the fact that he pointed to his research on his weblog. Interestingly I'm not the only one who was interested, as after I pointed to it on my link round up a few people asked if they could get a copy of the paper (yes, I almost always send papers if I have access). Luckily it's a nicely elegant piece of work, basically quantifying what we've already probably known qualitatively. There isn't that great of a value-add to quantification as such, but with a mathematical understanding of a topic one can engage in an algebra of mental manipulations so as to construct models with which one can project other facts. Quantitative information is often an excellent way to generate "free information" from theoretical models. The figure above is the primary result of the paper. Basically Arbesman took a data set which was laying around which measured the lengths of various empires (N = 41), and showed that the rise and fall of these political entities tends to follow an exponential distribution: e^−λt . This is an incredibly elegant summation of what we know qualitatively: some empires last a long time, but most do not.
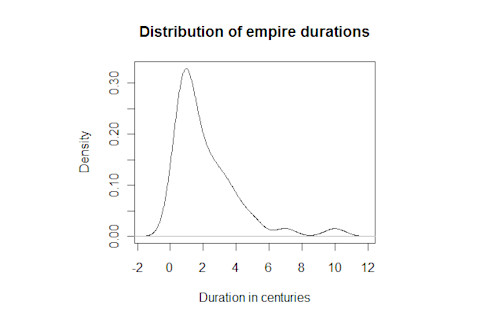
Interestingly the mean length of an empire is 220 years. That's basically what you'd probably expect from intuition, especially if you knew Chinese history. To the left is a density plot I generated with the data provided in the paper. You can see that the mode and mean are a bit different because of the skewness. One of the interesting points about the exponential distribution is that it implies that the the duration of an empire at any given moment can't tell you the probability that it's going to collapse in the near future. The distribution is "memoryless." In other words, the likelihood of doom striking isn't greater as time passes. This seems somewhat counterintuitive. After all doesn't the cohesion and elan of the a ruling caste of a given empire wane as the society slowly lose its vital force? Hasn't the author read Spengler! Arbesman admits that there are more complex equations which can describe the distribution more precisely, but the exponential formula has only one parameter, so it's quite parsimonious. But even if we have a first approximation we don't have a total description. Like evolutionary process as a whole I'm not convinced that the nature of the current data set is sufficient to deny the shifting background parameters which are operative over time. As I've noted before, there are two counteracting tendencies over time in human history when it comes to social & political entities: - A greater rate of cultural change over time - A greater cohesion and integrative power of social and political systems (more rapid bounce-backs from collapse, and greater civilizational continuity) One thing I wanted to do is check to see what the correlation between age of the polity and its duration was. My intuition was that older polities will have greater recorded duration. Obviously there's just more time for them, but some societies, such as Egypt, were very stable for longer periods of time in far antiquity. When I ran the correlate it was pretty weak, -0.23. Below is a chart which shows the scatter plot and the r-squared (correlation squared):
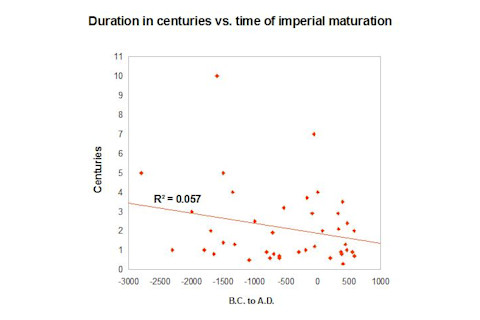
Here's the original data:
EmpireAdulthoodDuration
Western Turk (C. Asia)5820.7
Avar (Europe)5802
T'u Chueh Turk (C. Asia)5500.9
Visigoth (Europe)4702.4
White Hun (Indo-Iran)4601
Toba (China)4401.3
Yuen-Yuen (C. Asia)4000.3
Byzantine (Europe)3953.5
Hun (Europe)3800.8
Gupta (India)3700.9
Liu-Sung (China)3302.1
Ptolemaic (Africa)3232.9
Bactria (Indo-Iran)2000.6
Kushan (Indo-Iran)752
Rome (Europe)04
Saka (Indo-Iran)-501.2
Parthia (Iran)-607
Ch'in (China)-902.9
Andhra (India)-1703.7
Hsiung Nu Hun (C. Asia)-1901
Maghada-Maurya (India)-3000.9
Achaemenid (Iran)-5403.2
Lydia (Anatolia)-6100.6
New Babylon (Mesopotamia)-6100.7
New Assyrian (Mesopotamia)-7000.8
Late Period (Egypt)-7151.9
Phrygia (Anatolia)-7600.6
Urartu (Mesopotamia)-8100.9
Babylon (Mesopotamia)-10002.5
Middle Assyrian (Mesopotamia)-10900.5
Hittite (Anatolia)-13201.3
Hsia-Shang (China)-13504
New Empire (Egypt)-15005
Mitanni (Mesopotamia)-15001.4
Elam (Mesopotamia)-160010
Hykso (Syria)-16500.8
Babylon—Hammurabi (Mesopotamia)-17002
Old Assyria (Mesopotamia)-18001
Middle Empire (Egypt)-20003
Akadia (Mesopotamia)-23101
Old Empire (Egypt)-28005